P versus NP

This post is an introduction for understanding some important and unsolved problems in Computer Science and reasons why they matter. I’m assuming you know a bit about Turing machine - in short words it’s an abstract machine, which can simulate any algorithm we can write in any programming language using current model of computation (so for example on your computer).

Matters in this post are quite hard to explain, so if you want me to elaborate more, just ask in comments.

In Computer Science scientists divided set of all problems to subsets based on their complexity. As every problem can be stated as decision problem. Let’s consider only these.

Decision problems are these which have an output: YES or NO.

The most known sets of decision problems are \(NP\), \(P\) and \(PSPACE\) and these sets I want to describe.

\(P\) problems

Problems in \(P\) are those, which can be solved using polynomial time by deterministic Turing machine.

Intuitively you can think that for problem in \(P\) it’s possible to write an algorithm which will use polynomial time to solve it. Some common \(P\) problems are:

• greatest common divisor
• minimum in list
• shortest path problem

Here is an example of finding minimum in list problem in Erlang language:

    min([]) -> error;
    min([H|T]) -> min_helper(T, H).

    min_helper([], CurrentMin) -> CurrentMin;
    min_helper([H|T], CurrentMin) when CurrentMin > H ->
      min_helper(T, H);
    min_helper([_|T], CurrentMin) ->
      min_helper(T, CurrentMin).

We can see that it uses \(O(n)\) time, because we iterate in min_helper function over input list exactly once. It just picks head H of list - if it’s less than minimum then puts it in accumulator CurrentMin. Then it does the same for the tail of list. When we finally reach an empty list it returns minimum which is in CurrentMin accumulator.

\(NP\) problems

\(NP\) (Nondeterministic Polynomial time) problems are these for which we can verify if a solution is correct using polynomial time.

In other words for \(NP\) problems we will need a non-deterministic Turing machine to solve them in polynomial time for sure (such machine exists only in theory). This also means that when solving problem in \(NP\) using deterministic Turing machine we might need an exponential time. Be aware that all \(P\) problems are also in \(NP\) set, because we can use actual solving method as verification.

The most known \(NP\) problems are:

• traveling salesman problem - very common in real life!
• boolean satisfiability problem (\(SAT\)) - very important for AI
• vertex cover problem

These problems are \(NP\)-complete which means that they are in \(NP\) set and every problem in \(NP\) is not harder than any of these problems. None of \(P\) problems are \(NP\)-complete.

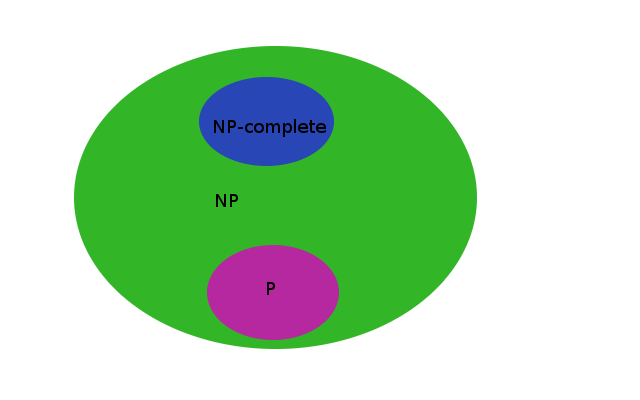
\(NP\)-complete problems are usually in exponential time, but keep in mind, that it’s not by their definition. They can be also in subexponential time.

\(PSPACE\) problems

\(PSPACE\) problems are these, which can be solved by deterministic Turing machine using polynomial space (memory).

Note that this time we are talking about space (memory) instead of time! Some examples:

• Quantified Boolean formula problem (\(QBF\))
• Reversi (game)
• Checkers (game)
• Mahjong (game)
• Chess and GO (when we have constraint for number of moves, otherwise they are proven to be even harder than \(PSPACE\))

\(P\) versus \(NP\)? What about \(PSPACE\)?

Currently scientists have proven that between \(P\), \(NP\) and \(PSPACE\) sets of problems there is a relation:

Inclusion can be intuitively understood as being easier relation. So any problem in \(P\) is easier than any problem which is in \(NP\) and not in \(P\). By easier intuitively I mean that we can write an algorithm to solve this problem, which will use less time to give solution. For example algorithms which solve problems in \(P\) can take for example \(O(n)\) time (for example: finding minimum in list) while those which solve \(NP\)-complete problems are usually in exponential time.

For me on the first sight wasn’t obvious why \(NP \subseteq PSPACE\). But when I thought that you can iterate for exponential time using polynomial space, it became clear that \(PSPACE\) problems are definitely not easier than problems in \(NP\).

We still don’t know if these two relations are only inclusions or equalities (there are some papers on \(NP\)=\(PSPACE\) for example NP = PSPACE, but there are a lot of discussions on them). If there will be a prove that \(P=NP\) then all our cryptography (SSL) will be unsafe. Proof of equality \(P=PSPACE\) will have big impact on Artificial Intelligence algorithms, but I want to cover it in next posts.

To be continued…

Next time I will describe some important problems for automated theorem proving like \(SAT\) and \(QBF\). The last one is also important for AI. I’m thinking about writing my own \(SAT\)-solver.

If you want me to cover something specific about this stuff or elaborate more don’t hesitate to leave a comment!